Polygonal-Light Shading

19 Feb 2019

polygonal-light shading

Definition and Properties

$D_{0}$ denotes the original distribution to be transformed. To generate a new distribution $D_{0}$, a linear transformation represented by a 3x3 matrix $M$ is applied to the direction vector $w_{0}$ of the original distribution $D_{0}$, where we get $w=\frac {Mw_{0}}{\left | Mw_{0}\right |}$.

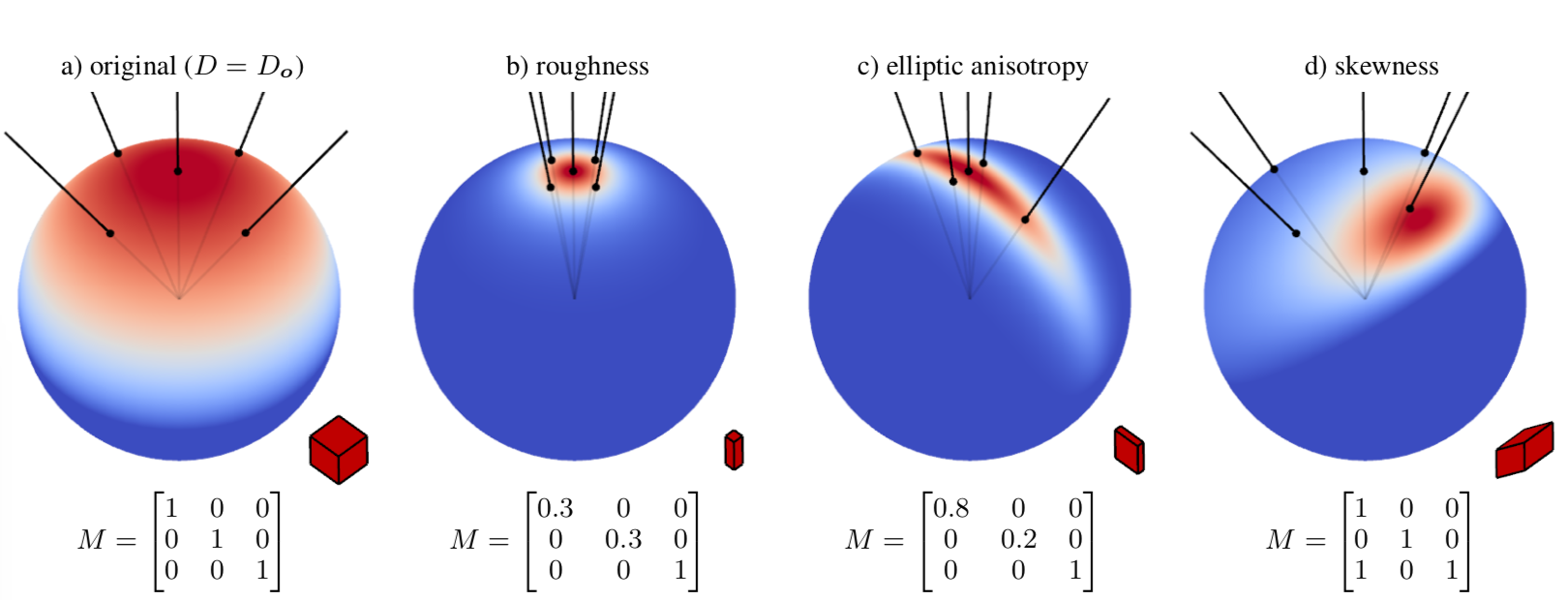
The magnitude of an LTSD is the magnitude of the original distribution $D_{0}$ in the original direction $w_{0}$ multiplied by the change of solid angle measure due to the distortion of the spherical transformation. It has the closed-form expression:

$$D(w)=D(w_{0})\frac {\partial w_{0}}{\partial w}=D_{0}(\frac {M^{-1}w}{\left \| M^{-1}w\right \|})\frac {\left | M^{-1}\right |}{\left \| M^{-1}w\right \|^{3}}$$

where $\frac {\partial w_{0}}{\partial w}=\frac {\left | M^{-1}\right |}{\left | M^{-1}w\right |^{3}}$ is the Jacobian of the transformation of normalized direction vectors $w=\frac {Mw_{0}}{\left | Mw_{0}\right |}$. The distribution is invariant to scaling transformations $(M = \lambda I )$ since scaling vectors doesn’t change their directions. Furthermore, rotations only change the orientation of the distribution, not its shape. This is because the Jacobian of the spherical transformation is constant if $M$ is a scaling or rotation matrix: $\frac {\partial w_{0}}{\partial w}=1$. The transformed distribution $D$ inherits several properties of the original distribution $D_{0}$. Properties of are listed below:

Normalization The norm of an LTSD $D$ is the norm of its original distribution $D_{0}$.

$$\int _{\Omega }D(w)dw=\int _{\Omega }D(w_{0})\frac {\partial w_{0}}{\partial w}dw=\int _{\Omega }D_{0}(w_{0})dw_{0}$$

Integration over Polygons The integral of an LTSD $D$ over a polygon $P$ is the integral of the original distribution $D_{0}$ over the polygon $P_{0} = M^{-1}P$ obtained by applying the inverse transformation $M^{-1}$ to each vertex of the polygon:

$$\int _{P}D(w)dw=\int _{P_{0}}D_{0}(w_{0})dw_{0}$$

Important Sampling Because $D$ is $D_{0}$ multiplied by the Jacobian of the transformation, the probability density function(PDF) of the sample $w$ is exactly $D(w)$.

$PDF(w_{0})=D_{0}(w_{0}) \Rightarrow PDF(w)=D_{0}(w_{0})\frac {\partial w_{0}}{\partial w}=D(w)$

Approximating Physically Based BRDFs with Linearly Transformed Cosines

Define the original distribution $D_{0}$ which is a normalized clamped cosine distribution in the hemisphere given by the z-direction:

$$D_{0}(w_{0} = (x, y, z)) = \frac{1}{\pi}max(0, z)$$

Approximate the spherical functions given by the cosine-weighted GGX BRDFs over the light directions $w_{l}$:

$$D \approx f(w_{v}, w_{l}) cos\theta _{l}$$

Assume an isotropic material, the BRDF depends on the incident direction $w_{v} = (sin\theta _{v}, 0, cos\theta _{v})$ and the roughness parameter $\alpha$. A matrix $M$ could yield the best fit with a Linearly Transformed Cosine. Because of the planar symmetry of isotropic BRDFs and Linearly Transformed Cosine’s scale invariant, the Matrix $M$ can be represented as:

$$M =\begin{bmatrix} a&0&b\\ 0&c&0\\ d&0&1 \end{bmatrix}$$

So only 4 parameters need to be fitted. More detail about the representation and storage, please see the paper.

Real-Time Polygonal-Light Shading with Linearly Transformed Cosines

Shading with diffuse polygonal lights means computing the illumination integral over a polygonal domain:

$$I = \int_{P}L(w_{l})f(w_{v}, w_{l}) cos\theta _{l}dw_{l}$$

then an approximation can be derived:

$$I = \int_{P}L(w_{l})f(w_{v}, w_{l}) cos\theta _{l}dw_{l} \approx \int_{P}L(w_{l})D(w_{l})dw_{l}$$

Shading with Constant Polygonal Lights

If the radiance emitted by the polygonal light is spatially constant, it means $L(w_{l})=L$. Then it becomes a separable multiplication factor of the integral:

$$I \approx \int_{P}L(w_{l})D(w_{l})dw_{l} = L\int_{P}D(w_{l})dw_{l}$$

because we have the polygonal integration property above, the integration can be simplified to:

$\int _{P}D(w)dw=\int _{P_{0}}D(w_{0})dw_{0}=E(P_{0})$

where $E$ is the irradiance of the polygon $P_{0} = M^{-1}P$. Since $D_{0}$ is a clamped cosine distribution, its integral over a polygon is the irradiance of this polygon, which has a closed-form expression:

$$E(p_{1},...,p_{n})=\frac {1}{2\pi }\sum _{i=1}^{n}acos(\left \langle \boldsymbol{p}_{i}, \boldsymbol{p}_{j}\right \rangle)\left \langle \frac{\boldsymbol{p_{i}}\times \boldsymbol{p_{j}}}{\left \| \boldsymbol{p_{i}}\times \boldsymbol{p_{j}}\right \|}, \begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}\right \rangle$$

with $j = (i + 1)\space mod\space n$.

Shading with Textured Polygonal Lights

Reference

Eric Heitz, J., S., D. Real-Time Polygonal-Light Shading with Linearly Transformed Cosines